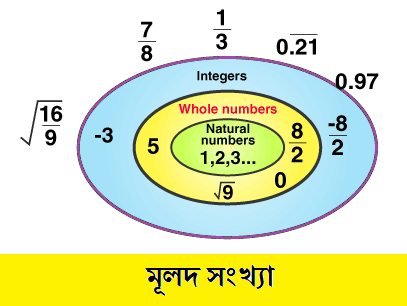
যেসব সংখ্যাকে p/q আকারে প্রকাশ করা যায়, যেখানে p এবং q পূর্ণসংখ্যা এবং q শূন্য (0) নয়, ওই সংখ্যাকে মূলদ সংখ্যা বলা হয়।
যেসব সংখ্যাকে ভগ্নাংশ আকারে প্রকাশ করা যায়, যেখানে হর এবং লব পূর্ণসংখ্যা এবং হর শূন্যের সমান নয়, তাকে মূলদ সংখ্যা বলে ।
এছাড়াও, আমরা বলতে পারি যে কোনো ভগ্নাংশ মূলদ সংখ্যার হতে পারে,
যেমন : যেকোনো পূর্ণসংখ্যা (৫) এবং সসীম এবং পৌণপৌনিক ভগ্নাংশ (৪/৫ কিংবা ৫.৩৩) এগুলি হলো মূলদ সংখ্যার উদাহরণ।পূর্ণসংখ্যাগুলিও মূলদ সংখ্যা কারণ যেকোনো পূর্ণসংখ্যাকে(৮) ভগ্নাংশ আকারে (৮/১) লেখা যায়।
মূলদ সংখ্যার উদাহরণ
- ৪
- 1/2
- -6/8
- 0.141414… বা 14/99
- -0.7 বা -7/10
- 0.3 বা 3/10
| p | q | p/q | মূলদ সংখ্যা |
|---|---|---|---|
| 100 | 20 | 100/20 = 5 | মূলদ সংখ্যা |
| 10 | 1000 | 10/1000 = 0.01 | মূলদ সংখ্যা |
| 500 | 20 | 500/20 = 25 | মূলদ সংখ্যা |
| 50 | 10 | 50/10 = 5 | মূলদ সংখ্যা |
| 10 | 1 | 10/1 = 10 | মূলদ সংখ্যা |
| 10 | 3 | 10/3 = 3.3 (এখানে দশমিকের পরে 3 যেহেতু বার বার পুনরাবৃতি হচ্ছে তাই পৌনপৌনিক ব্যবহার করা যেতে পারে দশমিকের পরে 3 এর মাথায়) | মূলদ সংখ্যা |
| 22 | 7 | 22/7 = 3⋅14159265… অর্থাৎ অসীম সংখ্যা যা পৌনপৌনিক ব্যবহার করা হয়। | অমূলদ সংখ্যা |
মূলদ সংখ্যা চেনার উপায়
১) সকল পৌণপৌনিক সংখ্যা মূলদ সংখ্যা। যেমন:- ৭.৩৩৩৩৩… কে ৭.৩ এর মাথায় পৌণপৌনিক ব্যবহার করা হয় যা একটি মূলদ সংখ্যা।
২) প্রত্যেক পূর্ণসংখ্যা একটি মূলদ সংখ্যা। যেমন ৭ একটি মূলদ সংখ্যা, কারণ ৭ কে ভগ্নাংশ আকারে লেখা যাবে ৭/১, আমরা এটাও জানি সকল পূর্ণ সংখ্যার নিচে ১ থাকে।
৩) এটি p/q আকারে উপস্থাপিত হয় , যেখানে q≠0 (অর্থাৎ q এর মান শূন্য নয়)।
৪) অনুপাত p/q আরও সরলীকৃত এবং দশমিক আকারে উপস্থাপন করা যেতে পারে।
৫) ধনাত্মক, ঋণাত্মক সংখ্যা, শূন্য, স্বাভাবিক সংখ্যা, প্রকৃত ও অপ্রকৃত ভগ্নাংশ সকলেই মূলদ সংখ্যা।
৬) যদি দশমিকের পরের ঘরগুলো সসীম হয় অর্থাৎগণনা করা যায়, তবে সংখ্যাটি হবে মূলদ সংখ্যা। যেমন:- ৯.৮৪ এবং ৭২১.৭৩ ইত্যাদি।
৭) যদি দশমিকের পরের ঘরগুলো অসসীম হয় কিন্তু একই সংখ্যার পুনরাবৃতি হয়, তাহলে সংখ্যাটি হবে মূলদ সংখ্যা। যেমন : ৯.৬৫৬৫৬৫ অর্থাৎ এটিকে ৯.৬৫(দশমিকের পরে ৬৫ এর মাথায় পৌণপৌনিক লাগাতে পারি)। এছাড়াও ৮.৩৩৩৩৩ এরকম একই সংখ্যা থাকলে তাহলে ৩ এর মাথায় পৌণপৌনিক ব্যবহার করতে পারি। এই সমস্ত সংখ্যাগুলি হলো মূলদ সংখ্যা।
৮) যে কোন পূর্ণবর্গ সংখ্যার বর্গমূল হলো মূলদ সংখ্যা। যেমন:- √২৫ এবং √১৬
0 একটি মূলদ সংখ্যা?
দশমিক আকারে মূলদ সংখ্যা
যেমন ২.২ কে ২২/১০ আকারে লেখা যেতে পারে।
এখন 0.333 এর মতো অসমাপ্ত দশমিক সম্পর্কে কথা বলা যাক। যেহেতু 0.333… 1/3 হিসাবে লেখা যেতে পারে, তাই এটি একটি মূলদ সংখ্যা।
অর্থাৎ দশমিক সংখ্যার পরে যদি একটি সংখ্যা কিংবা কয়েকটি সংখ্যার পুনরাবৃতি হতে থাকে তাহলে ওই সংখ্যাটি মূলদ সংখ্যা হবে।
যেমন ৫.৬২৬২৬২ (এখানে দশমিকের পরে ৬২ এর পুনরাবৃতি হচ্ছে বার বার তাই এটি মূলদ সংখ্যা) আবার ৪.৬৬৬৬৬৬৬ এরকম সংখ্যাও মূলদ সংখ্যা।
কিন্তু যদি আলাদা আলাদা অসীম সংখ্যা দশমিকের পরে থাকে। তাহলে ওই সংখ্যা মূলদ সংখ্যা হবে না। ওই সংখ্যা অমূলদ সংখ্যা হবে।
মূলদ সংখ্যার শ্রেণীবিভাগ
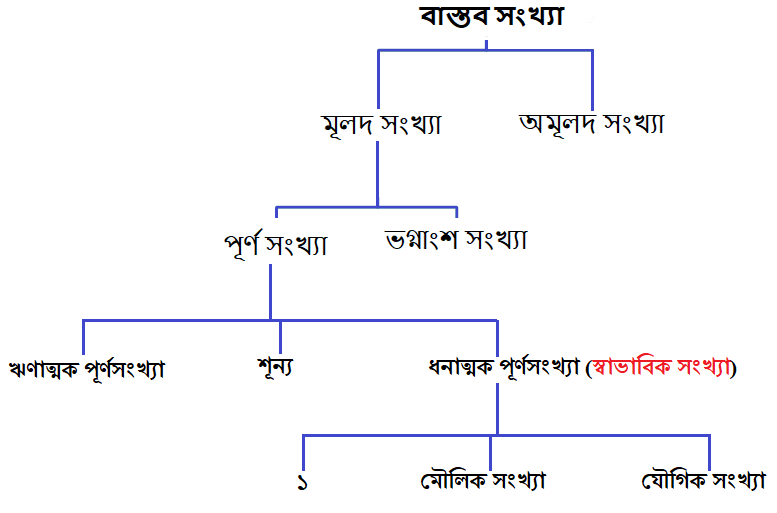
১. পূর্ণ সংখ্যা কাকে বলে? শ্রেণীবিভাগ সমন্ধে বিস্তারিত আলোচনা করা হলো।
২. ভগ্নাংশ কাকে বলে?


